Привет, дорогой читатель! Я рад, что вы открыли эту статью, потому что я хочу рассказать о чем-то очень интересном и удивительном. Вы когда-нибудь задумывались, почему некоторые произведения искусства и инжиниринга так притягательны для глаза, а другие - нет? Когда говорят об искусстве, математика, кажется, может быть далека от этого мира творчества.
Наверное, думаете, что математика - это скучная и сухая наука, которая не имеет ничего общего с искусством. Представляете себе математиков и инженеров как серых и занудных людей, которые сидят за своими формулами и диаграммами, не замечая красоты мира. Считаете, что искусство - это сфера творчества и воображения, которая не поддается логике и расчетам. Вы, ошибаетесь.Понимание математики и природы это путь к открытию удивительной красоты, восторг которой равен величайшему искусству.

Да, я знаю, что это звучит провокационно и дерзко, но я хочу вас удивить и заинтересовать. На самом деле, математические принципы и вычисления часто лежат в основе некоторых из самых впечатляющих искусственных произведений. Ответ на эти вопросы может быть неожиданным: геометрия и математика. Да, вы не ошиблись, математика - это не только скучная наука о числах и формулах, но и источник красоты и творчества. В этом эссе я расскажу вам, как математика используется в разных видах искусства, и как она помогает художникам и инженерам создавать потрясающие произведения.
Вот несколько интересных аспектов того, как математика используется в художественных приемах:Пропорции и Гармония.
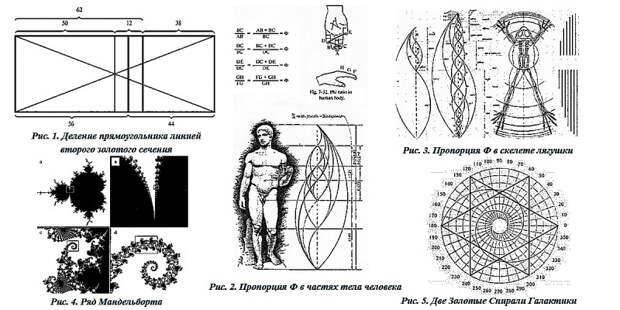
Одним из наиболее известных математических концепций, которые находят применение в искусстве, являются золотое сечение и пропорции Фибоначчи.
Золотое сечение - это отношение двух величин, при котором отношение суммы этих величин к большей из них равно отношению большей величины к меньшей. Звучит сложно, но на самом деле это очень просто. Представьте себе отрезок, который разделен на две части так, что отношение длины всего отрезка к длине большей части равно отношению длины большей части к длине меньшей части. Это и есть золотое сечение. Его значение приблизительно равно 1,618. Это число называют золотым числом или числом Фи.
Пропорции Фибоначчи - это последовательность чисел, в которой каждое следующее число равно сумме двух предыдущих. Например, 1, 1, 2, 3, 5, 8, 13, 21, 34 и так далее. Эта последовательность названа в честь итальянского математика Леонардо Фибоначчи, который ввел ее в своей книге «Liber Abaci» в 1202 году. Но самое интересное, что если вы разделите каждое число этой последовательности на предыдущее, то вы получите приближенное значение золотого числа. Например, 8/5 = 1,6; 13/8 = 1,625; 21/13 = 1,615 и так далее.

Таким образом, золотое сечение и пропорции Фибоначчи - это две стороны одной медали. Они связаны между собой математической закономерностью и обладают эстетической силой. Например, знаменитая картина Леонардо да Винчи «Мона Лиза» построена на принципе золотого сечения. Ее лицо, тело, фон и даже улыбка соответствуют золотым пропорциям. А великий архитектор Андреа Палладио использовал пропорции Фибоначчи в своих зданиях, таких как вилла Ротонда в Италии. Он считал, что эти пропорции создают идеальную гармонию и красоту.
Эти пропорции обладают особым визуальным очарованием и используются в архитектуре, живописи, дизайне и других видах искусства для создания гармоничного баланса и приятного восприятия. Пирамида Хеопса, Парфенон, Нотр-Дам, Тадж-Махал, Эйфелева башня и многие другие знаменитые сооружения построены с учетом золотого сечения и пропорций Фибоначчи, чтобы создать гармоничный и впечатляющий вид.
Возможно, вы удивитесь, но золотое сечение и пропорции Фибоначчи можно найти не только в искусстве, но и в природе. Вы когда-нибудь замечали, как растут листья на ветке, или как расположены лепестки на цветке? Это не случайно, а следствие математического закона, который определяет оптимальное распределение пространства и ресурсов. Не правда ли, это удивительно?
Тектоника - это принцип, который подразумевает, что форма определяется конструкцией. При этом конструкция становится средством формообразования с композиционными и пластическими свойствами. Тектоника позволяет выразить в форме вещи ее внутреннюю сущность, ее функциональное и технологическое назначение, ее прочность и устойчивость. Тектоника также способствует экономии материалов и энергии, а также упрощению производства и сборки вещи.
Другой распространенный метод — перспектива, которая также основана на математических принципах для создания иллюзии трехмерности на плоском холсте. Итальянский художник и архитектор эпохи Проторенессанса Джотто ди Бондоне был одним из первых, кто начал применять законы перспективы в работах.

Я надеюсь, что вы не заснули от моих умных рассуждений. Или, может быть, вы уже перестали читать этот текст, потому что он вам показался слишком асимметричным? Симметрия… Что это такое? Почему мы так любим все, что симметрично? На самом деле, симметрия очень часто встречается в нашей жизни. Мы сами создаем симметричные предметы, потому что они нам нравятся. Например, здания, мебель, одежда, украшения, логотипы и т.д. Мы думаем, что симметрия придает им гармонию, порядок, красоту.

Но не думайте, что симметрия – это абсолют. Нет, симметрия – это относительное понятие. Все зависит от того, с какой точки зрения мы смотрим на вещи. Например, если мы посмотрим на человеческое тело сбоку, мы увидим, что оно не симметрично. У нас есть одно сердце, одна печень, один желудок и т.д. Но если мы посмотрим на тело спереди, мы увидим, что оно почти симметрично. У нас есть два глаза, два уха, две руки, две ноги и т.д. То же самое можно сказать о лице. Если мы проведем по нему вертикальную линию, мы увидим, что левая и правая стороны похожи, но не идентичны. У каждого из нас есть свои особенности, которые делают нас уникальными.
Но немного хаоса и уникальных черт не сделают его несовершенным. Они сделают его более очаровательным для нашего восприятия. Симметрия также широко встречается в природе. Мы можем найти ее во многих формах и проявлениях. Например, снежинки, кристаллы, падающие дождевые капли, которые имеют форму сферы, радужная оболочка мыльного пузыря, цветы, раковины, бабочки, звезды и многое другое.
Современный человек просто не в состоянии представить себе несимметричный (а значит, и нефункциональный) самолет или автомобиль. В этой связи показательны наблюдения известного летчика-испытателя, Героя Советского Союза Марка Галлая: "Я заметил, что красивая, ласкающая своими пропорциями взор машина обычно к тому же и хорошо летает. Эта, на первый взгляд, почти мистическая закономерность имеет, я думаю, свое вполне рациональное объяснение: дело, по-видимому, обстоит как раз наоборот - хорошо летающая машина начинает представляться "красивой". Эстетическое формируется под влиянием рационального".
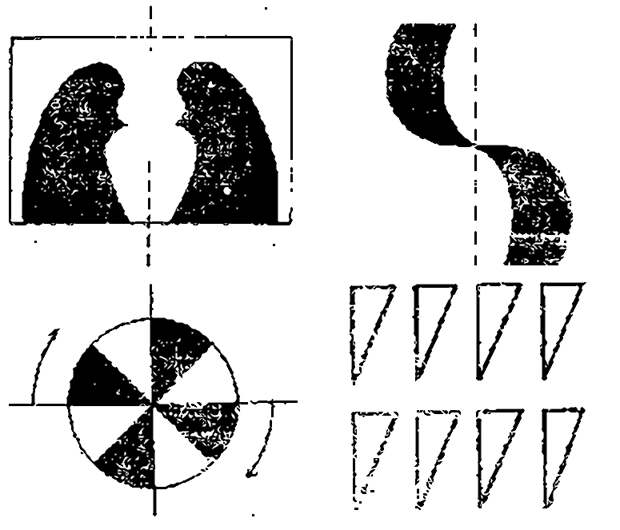
Симметричные и асимметричные элементы могут сочетаться в одной композиции. В этом случае она основывается на подчинении второстепенных, несимметричных частей главной симметричной форме. Такое подчинение обеспечивает визуальное равновесие всей композиции. Оно достигается, когда центральный элемент не совпадает с общей формой, а ее составляющие – совпадают, или наоборот.
Самый сложный случай – создание композиционного равновесия между элементами, у которых оси симметрии находятся в различных координатных плоскостях. Для того, чтобы сделать эти композиции гармоничными, нужно обладать глубоким чувством пропорций и знанием законов симметричного формирования.
Ритм и метр - это композиционные средства, которые часто используются в сочетании с пропорцией. Ритм - это повторение с изменениями, а метр - это повторение без изменений. Ритм и метр позволяют создавать динамичные и гармоничные формы, а также упорядочивать и структурировать пространство. Ритм и метр могут быть простыми, когда меняется одна характеристика (форма, цвет, расстояние между элементами и т.п.) и сложными, когда изменения затрагивают несколько характеристик одновременно.
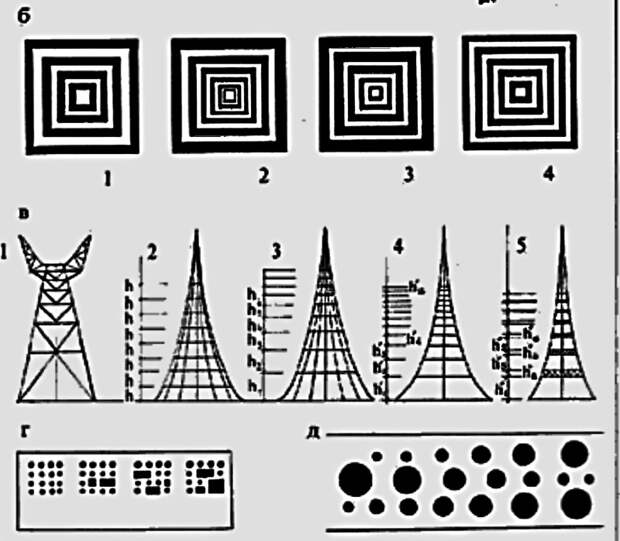

Также важно, какой направленности ритм – горизонтальной или вертикальной. Развитие по вертикали упрощает композиционные задачи: обычно, изменения по вертикали сами по себе способствуют появлению зрительного завершения. А если ритм развивается по горизонтали, то возникает проблема завершения и начала композиции. Для создания простейшего метрического или ритмического ряда необходимо не менее трех-четырех элементов, образующих непрерывное ритмическое движение. Увеличение числа элементов усиливает наглядность ритма, однако при их большом количестве может возникнуть скучное однообразие.
Вероятно, из всех средств композиции ритм наиболее связан с психофизиологией восприятия, и это понятно: ведь нарушение ритмического ряда выглядит как явление явно негативное, как нарушение очень строгой закономерности. Будь то конструирование ажурной телебашни или простой вентиляционной решетки с постепенным уменьшением размеров колец и просветов, необходимо следить, чтобы ничто не нарушало закономерности ритма.
Эргономика (от греч. ergon — работа и nomos — закон) — научная теоретическая и научно-экспериментальная дисциплина, изучающая психофизиологические факторы взаимодействия человека и техники в рамках единой системы «человек-машина». Эргономика стремится минимизировать негативные воздействия условий труда на нервную систему человека и его работоспособность, а также повысить комфорт, безопасность и эффективность использования техники. Эргономика учитывает анатомические, физиологические, психологические и социальные особенности человека, а также его индивидуальные и групповые потребности.
Цвет - это не только визуальный, но и образно-ассоциативный и эмоциональный феномен. Цвет оказывает влияние на настроение, восприятие, память, внимание, мышление, поведение человека. Цветовые гармонии - это закономерности сочетания цветов, которые создают приятное, красивое и согласованное впечатление. Цветовые гармонии могут быть основаны на контрасте, аналогии, монохромии, комплементарности, триаде и т.д. Цветовая система, которую в начале XX века разработал немецкий ученый Вильгельм Оствальд, состояла из 8 цветовых оттенков, основанных на четырех основных цветах: желтом, ультрамариновом синем, красном и зеленом (цвете морской волны). Из этих цветов получался цветовой круг из 24 цветов – цветовой круг Оствальда, где он искал математические принципы цветовой гармонии, основываясь на геометрических соотношениях между цветами внутри круга. По мнению Оствальда, гармоничными были все цвета, в которых присутствовало одинаковое количество белого или черного цвета, а среди тех, в которых такого количества не было, наибольшую гармонию имели те, которые находились в цветовом круге на равном расстоянии друг от друга.
Симметрия, пропорции, ритм, контраст, цельность - составляющие гармонии объективно связаны с природой, с движением и развитием материи. Наши эстетические взгляды тесно связаны с этими понятиями. Однако, социальное существование человека в разные эпохи под разным углом зрения рассматривало категории гармонии и это определяло их роль в общественной жизни и в искусстве. Представление о прекрасном эволюционировало, изменялось. Гармония стала рассматриваться не как количественный, а как качественный принцип, соединяя физическое и духовное начала. Если древние греки считали прекрасным только упорядоченное и всякое нарушение симметрии и пропорций находили безобразным, то в последующие эпохи проявления прекрасного стали обнаруживать и в нарушении порядка, в диссонансах, в кажущейся дисгармонии, ибо они свойственны жизни и, следовательно, являются частью какой-то иной гармонической системы, в которой обретают логику и смысл. «Прекрасное - есть жизнь»,- писал Чернышевский. И она не стоит на месте. Появления гармонии в природе и жизни шире, чем это может охватить любой канон, любая гармоническая система. И человечество никогда не перестанет искать новых гармонических отношений, сочетаний, искать проявления иных гермонических закономерностей. Однако, это не значит, что классическая гармония потеряла свое значение. То, что уже открыто, те найденные закономерности, их математическое обоснование, остаются вечным достоянием человечества, из которого будут черпать все последующие поколения.
Геометрические Формы.
Вы, наверное, знаете, что геометрия - это наука о формах и их свойствах. Вы, наверное, помните, как в школе рисовали окружности, треугольники, квадраты, многогранники, пирамиды, цилиндры, шары, сферы и другие фигуры. Думаете, что это было скучно и бесполезно. Знайте, что геометрические формы - это не только учебный материал, но и художественный инструмент. Многие художники и инженеры дизайнеры используют геометрические формы, такие как окружности, треугольники, квадраты и спирали, для создания уникальных композиций и узнаваемого стиля. Эти формы часто имеют математическую основу и помогают добиться определенного эстетического эффекта. Выбирают определенные формы, чтобы передать определенное настроение, идею или эмоцию. Например, окружность - это символ совершенства, целостности, единства и бесконечности. Треугольник - это символ стабильности, силы, направления и динамики. Квадрат - это символ порядка, равновесия, симметрии и рациональности. Он часто используется в геометрическом абстракционизме, таком как кубизм, и в минимализме, таком как супрематизм.
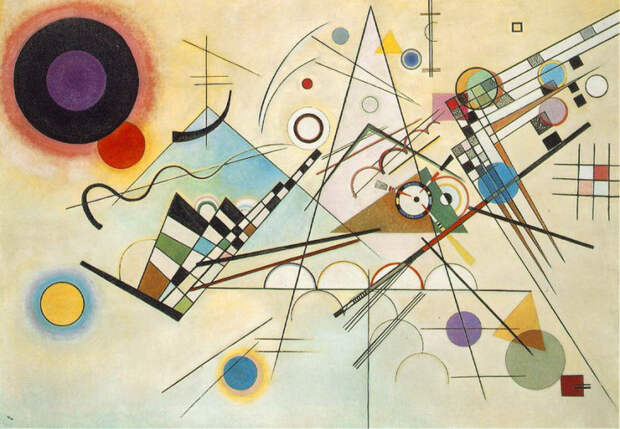
Геометрические формы могут быть очень разнообразными и творческими, если их комбинировать и изменять. Например, посмотрите на эти работы художника Василия Кандинского, который считается одним из основоположников абстрактного искусства. Он использовал простые геометрические фигуры, но придал им разные цвета, размеры и положения, создавая уникальные композиции, полные динамики и эмоций.
Наиболее известное описание правильных многогранников содержится в диалоге Платона «Тимей», приводятся конструкции четырех многогранников и говорится, что они олицетворяют четыре стихии: тетраэдр – это огонь, куб – земля, октаэдр – воздух, а икосаэдр – вода. Додекаэдр, согласно Платону, символизирует Вселенную.

Архимедовы тела отличаются от Платоновых тел (правильных многогранников), которые состоят только из одного типа многоугольников в одинаковых вершинах, и от многогранников Джонсона, правильные многоугольные грани которого принадлежат различным типам вершин.
Фракталы.
Фракталы - это сложные геометрические фигуры, которые могут быть построены с использованием математических алгоритмов. Они часто встречаются в современном искусстве и могут создавать потрясающие визуальные образы с бесконечной детализацией.
И вы не поверите, но они везде вокруг нас. В природе, в искусстве, в технологии, в музыке, в литературе.
А сейчас давайте определим, что же такое фракталы. Слово «фрактал» происходит от латинского «fractus», что означает «сломанный» или «раздробленный». Фрактал - это геометрическая фигура, которая состоит из множества частей, каждая из которых является уменьшенной копией целого. То есть, если вы возьмете фрактал и разобьете его на кусочки, то каждый кусочек будет выглядеть так же, как исходный фрактал, только меньше. И так можно продолжать до бесконечности, получая все более мелкие и мелкие копии. Это называется самоподобием, и это одна из основных характеристик фракталов.
Но самоподобие не единственное, что делает фракталы такими уникальными. Еще одна важная особенность фракталов - это их размерность. Вы, наверное, знаете, что в обычной геометрии есть три размерности: длина, ширина и высота. И вы, наверное, знаете, что линия имеет одну размерность, плоскость - две, а тело - три. Но что, если я вам скажу, что есть фигуры, которые имеют нецелые размерности? То есть, они не линии, не плоскости, и не тела, а что-то среднее. Например, 1,5 или 2,7. Звучит странно, не правда ли? Но это именно так. Фракталы имеют фрактальную размерность, которая может быть любым дробным числом.
Но откуда они взялись и как их можно построить? Для этого нам нужно обратиться к истории математики и встретиться с одним из ее гениев - Бенуа Мандельбротом.
Бенуа Мандельброт - это французский математик, который родился в 1924 году в Польше, а потом переехал во Францию, а затем в США. Он известен тем, что ввел термин «фрактал» и разработал теорию фрактальной геометрии.
Мандельброт был очень любознателен и интересовался разными явлениями, которые не поддавались обычной математике. Он заметил, что многие объекты в природе имеют сложную и неправильную форму, которая не может быть описана простыми уравнениями. Например, облака, горы, берега моря, деревья, листья, сосуды, легкие и т.д. Он задался вопросом: можно ли создать математическую модель, которая бы могла описать эти объекты?
Для этого он начал изучать разные математические конструкции, которые имели свойство самоподобия. Одна из них - это множество Кантора, которое было открыто в 1883 году немецким математиком Георгом Кантором. Множество Кантора - это пример фрактала, который можно построить следующим образом:
- Возьмите отрезок единичной длины и разделите его на три равные части.
- Удалите среднюю часть, оставив два отрезка длины 1/3.
- Повторите этот процесс для каждого из оставшихся отрезков, разделяя их на три части и удаляя среднюю.
- Продолжайте этот процесс до бесконечности.
В результате вы получите множество Кантора, которое состоит из бесконечного количества точек, расположенных на отрезке единичной длины. Это множество имеет несколько удивительных свойств:
- Оно имеет нулевую площадь, то есть оно не занимает никакого места на плоскости.
- Оно имеет бесконечную длину, то есть если вы попытаетесь измерить его, вы никогда не закончите.
- Оно имеет фрактальную размерность, равную логарифму 2 по основанию 3, то есть примерно 0,63. Это означает, что оно не является ни линией, ни плоскостью, а что-то между ними.
- Оно имеет свойство самоподобия, то есть если вы возьмете любой его кусочек, он будет выглядеть так же, как и целое множество.
Мандельброт был восхищен множеством Кантора и другими подобными конструкциями, которые называются множествами Жюлиа, множествами Фату, кривыми Коха, треугольниками Серпинского и т.д.

Он понял, что эти фракталы могут быть использованы для моделирования разных объектов в природе, которые имеют сложную и неправильную форму. Он также понял, что эти фракталы могут быть созданы с помощью компьютера, который может выполнять бесконечные итерации и рисовать полученные фигуры на экране.
Одним из самых известных фракталов, которые Мандельброт создал с помощью компьютера, является множество Мандельброта. Это множество состоит из точек на комплексной плоскости, которые удовлетворяют определенному условию. Комплексная плоскость - это система координат, в которой каждая точка имеет две составляющие: действительную и мнимую. Действительная составляющая соответствует горизонтальной оси, а мнимая - вертикальной. Комплексные числа - это числа, которые имеют действительную и мнимую часть. Например, 2 + 3i, где i - это мнимая единица, такая, что i^2 = -1.
Множество Мандельброта определяется следующим образом:
- Возьмите любое комплексное число c и начните с нуля: z_0 = 0.
- Вычислите следующее число по формуле: z_1 = z_0^2 + c.
- Повторите этот процесс, используя предыдущее число: z_2 = z_1^2 + c, z_3 = z_2^2 + c и т.д.
- Если последовательность z_n не стремится к бесконечности, то число c принадлежит множеству Мандельброта. Если же последовательность z_n уходит в бесконечность, то число c не принадлежит множеству Мандельброта.
Множество Мандельброта - это множество всех таких чисел c, которые не приводят к бесконечности. Если вы нарисуете это множество на комплексной плоскости, вы получите очень красивую и сложную фигуру, которая имеет форму сердца с бесконечным количеством усиков, изгибов и дырок. Эта фигура имеет свойство самоподобия, то есть если вы увеличите любую ее часть, вы увидите, что она повторяет форму целого множества, но с некоторыми изменениями. Эта фигура также имеет фрактальную размерность, которая равна примерно 2, несмотря на то, что она нарисована на плоскости.
Множество Мандельброта - это один из самых известных и красивых фракталов, который поражает своей сложностью и гармонией.
Оно стало символом фрактальной геометрии и вдохновило многих художников на создание своих произведений, используя фракталы как основу или элемент дизайна. Например, вы можете увидеть фракталы в работах таких художников, как Макс Эрнст, Сальвадор Дали, Эшер, Кинкейд, Хардинг и других. Они использовали фракталы для создания абстрактных, сюрреалистических или реалистических изображений, которые отражают их внутренний мир, фантазии или восприятие реальности.
Но фракталы не только в живописи. Они также присутствуют в других видах искусства, таких как скульптура, архитектура, музыка, литература и даже кино. Да, вы не ошиблись, фракталы есть и в кино. Вы когда-нибудь смотрели фильм «Матрица»? Если да, то вы наверняка помните сцену, когда главный герой Нео видит мир в виде зеленых цифр, которые складываются в разные формы. Это тоже фракталы. Или, например, фильм «Аватар», в котором показана планета Пандора с ее удивительной флорой и фауной. Вы заметили, как многие растения и животные имеют фрактальную структуру? Это не случайно. Это результат того, что создатели фильма использовали фракталы для генерации компьютерной графики, которая выглядит очень реалистично и красиво.

Вы уже захотели попробовать сами создать что-то с помощью математики и искусства? Тогда я рекомендую вам посетить online fractal creator, где вы можете научиться делать фракталы с помощью простых алгоритмов. Фракталы - это удивительные геометрические фигуры, которые повторяются на разных масштабах и имеют бесконечную детализацию. Они могут выглядеть как снежинки, деревья, облака или даже галактики.
ПО Ultra Fractal предлагает уникальный подход к созданию 2D-фракталов с использованием тысяч видов фракталов и алгоритмов окрашивания, а также с 64-битной поддержкой для глубокого масштабирования и возможностью комбинирования нескольких фракталов в одно изображение с помощью нескольких слоев, добавляя цвета с помощью градиентов. Не обязательно быть математиком, чтобы работать с этим инструментом, поскольку он предоставляет интуитивные средства для достижения желаемого результата.

Фрактальные структуры могут сделать изделия неповторимыми и придать им оригинальный облик.
Кодирование, Инженерные Решения и Интерактивное Искусство.
STEAM - акроним Science, Tecnology, Engineering, Art and Maths. Современные художники и программисты все чаще объединяют математику и искусство, создавая интерактивные инсталляции и алгоритмические произведения, которые реагируют на зрителя. Программирование и математические расчеты позволяют им создавать удивительные перформансы и визуальные эффекты.
Например, проект "Rain Room" дизайн-студии Random International использует код и датчики, чтобы создать впечатляющую арт-инсталляцию, позволяющую посетителям перемещаться в помещении, избегая дождя. "Комната дождя" представляет собой уникальную комнату площадью около 100 квадратных метров, оснащенную сотнями форсунок на потолке, из которых идет искусственный дождь объемом 1000 литров в минуту. Несмотря на обильный ливень, люди могут свободно проходить по комнате, не промокая. Это возможно благодаря использованию 3D камер, которые распознают человеческий контур и отключают форсунки над ним. Кроме того, установка Rain Room включает в себя литьевые плитки, электромагнитные клапаны, регуляторы давления, трехмерные камеры слежения, деревянные рамки, стальные балки и гидравлическую систему управления.

Еще один пример - Morphogenetic Creations, компьютерная выставка цифрового искусства с использованием программируемых алгоритмов Энди Ломаса, в Центре искусств Watermans, Лондон. Произведения, созданные с использованием математических алгоритмов и программирования, привносят в искусство цифровую интерактивность и динамику.

Конечно, вы можете подумать, что инжиниринг, математика и искусство - это совершенно разные вещи, и что у них нет ничего общего. Но это не так. На самом деле - это две стороны одной медали, которая называется креативность. Да, да, не удивляйтесь, математика тоже может быть креативной, если вы знаете, как ее применять. И наоборот, искусство тоже может быть логичным, если вы знаете, как его анализировать.
Когда мы видим какой-то предмет, мы обычно обращаем внимание на его форму, цвет, текстуру, материал, функциональность. Но за этими внешними характеристиками скрывается целый процесс инженерного проектирования, который учитывает множество факторов, связанных с жизненным циклом вещи: от ее производства до утилизации. Инженерный дизайн - это не просто создание вещей, а создание вещей с умом.
Инженерный дизайн основывается на комплексном системном подходе к проектированию каждой вещи. Это значит, что вещь рассматривается не изолированно, а в контексте ее взаимодействия с другими вещами, с человеком, с окружающей средой. Каждая вещь должна удовлетворять не только требованиям полезности и красоты, но и всем аспектам ее функционирования: эргономике, нагрузкам, транспортировке, упаковке, размещению, уходу, включению и т.д. Кроме того, каждая вещь должна соответствовать вкусам множества людей, так как инженерный дизайн создает предметы, производимые промышленно в больших количествах на станках. Исследование подтвердило гипотезу о том, что природные законы влияют на проектирование объектов (предметов) с рациональной и эстетичной структурой. Если при создании не соблюдать систематические законы, то это негативно повлияет на психоэмоциональное восприятие человека, и, в результате, у него не будет почти никакого интереса к спроектированному объекту (предмету), что приведет к отрицательному спросу. Инженерный чертеж детали - это не просто чертеж, а инженерное произведение искусства, которое будет отражать мою страсть к технологиям и инновациям. С техническим чертежом выполненным у меня вы сможете создать продукт, который будет востребован на рынке и удовлетворит самые высокие стандарты.
Вы, наверное, думаете, что я какой-то сумасшедший фанат математики, который видит ее во всем и везде. Но это не так. Я просто люблю инженерное дело и искусство и хочу показать вам, как оно связано с математикой, и как они взаимодействуют друг с другом. Не говорю, что вы должны стать инженерами или художниками, чтобы наслаждаться этими науками. Я говорю, что вы должны быть открытыми и любознательными, чтобы расширить свой кругозор и узнать что-то новое. И, конечно, чтобы получить удовольствие от процесса.